基本的图算法
图的表示
图$G=(V,E)$
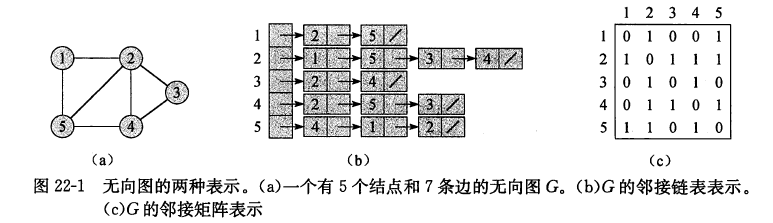
1、邻接链表
2、邻接矩阵
- 适合稠密图,或需要快速判断两个节点中是否有边时,或图规模较小时
存储需求:$\Theta(V^2)$
无向图的邻接矩阵是一个对称矩阵
广度优先搜索
- 结点颜色
- 运行时间:$O(V+E)$
- 性质:
- BFS计算出的v.d为s到v的最短路径距离
- 广度优先树:BFS搜索过程中生成的树

深度优先搜索

性质
括号化结构
- 对于两个结点u、v:
- 区间包含关系:在深度优先森林中具有祖先与后代关系
- 区间不相交:没有后代关系
有向图边的分类(图c)
- 树边:深度优先森林中的边
- 后向边(B):子孙指向祖先的边
- 前向边(F):祖先指向子孙的边
- 横向边(C):其他边
无向图中只有树边和后向边,没有前向边和横向边
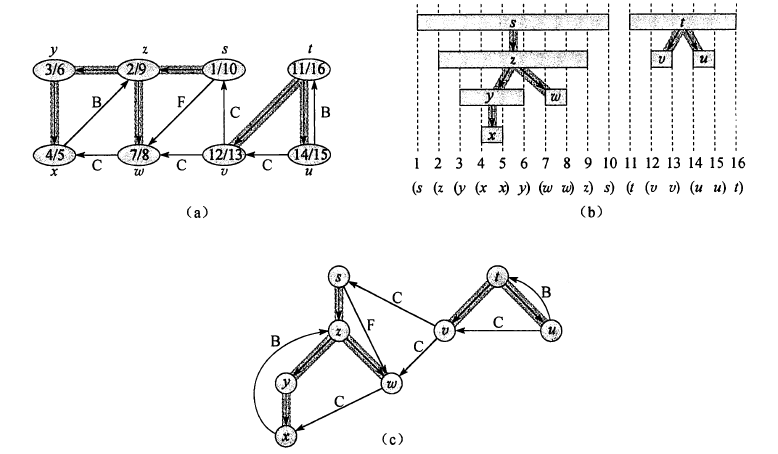
拓扑排序
- 拓扑排序:G中所有节点的一种线性次序,满足如果图G包含边(u,v),则节点u在拓扑排序中处于节点v的前面(如果图G包含环路,则不可能排出一种线性次序)
- 拓扑排序算法:与DFS完成时间顺序相反

在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
它是一个 DAG 图,那么如何写出它的拓扑排序呢?这里说一种比较常用的方法:
- 从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
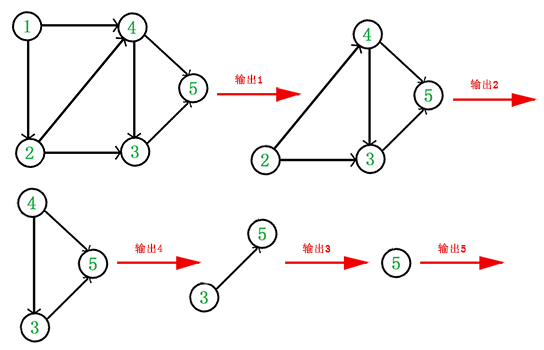
实现:(LeetCode 210 课程表II)
先建立一个邻接矩阵表示图,方便进行直接查找。拓扑排序也可以被看成是广度优先搜索的一种情况:我们先遍历一遍所有节点,把入度为0的节点(即没有前置课程要求)放在队列中。在每次从队列中获得节点时,我们将该节点放在目前排序的末尾,并且把它指向的课程的入度各减1;如果在这个过程中有课程的所有前置必修课都已修完(即入度为0),我们把这个节点加入队列中。当队列的节点都被处理完时,说明所有的节点都已排好序,或因图中存在循环而无法上完所有课程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph(numCourses, vector<int>());
vector<int> indegree(numCourses, 0);
for(vector<int> pair: prerequisites)
{
graph[pair[1]].push_back(pair[0]);
indegree[pair[0]] ++;
}
queue<int> Q;
vector<int> ans;
for(int i = 0; i < numCourses; i++)
{
if(indegree[i] == 0)
Q.push(i);
}
while(!Q.empty())
{
int p = Q.front();
Q.pop();
ans.push_back(p);
for(int neighbor: graph[p])
{
indegree[neighbor] --;
if(indegree[neighbor] == 0)
Q.push(neighbor);
}
}
if(ans.size() != numCourses)
return vector<int>();
return ans;
}
};
|
强连通分量
最小生成树
最小生成树:无向图中的一个边的子集,既能够将所有的结点连接起来,又具有最小的权重
Kruskal算法
在所有连接森林中两棵不同树的边里,找到权重最小的边(u,v)。使用并查集数据结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
struct Edge
{
int u, v;
int weight;
Edge(int s, int e, int w):u(s), v(e), weight(w){}
bool operator > (const Edge& e1) const
{
return weight > e1.weight;
}
};
int Kruskal(int N, vector<vector<int>>& connections)
{
priority_queue<Edge,vector<Edge>, greater<Edge>> min_heap;
for(vector<int> e: connections)
{
min_heap.push(Edge(e[0] - 1, e[1] - 1, e[2]));
}
UFSet ufset(N);
int count = 0;
int ans = 0;
while(count < N && !min_heap.empty())
{
Edge e = min_heap.top();
min_heap.pop();
int r1 = ufset.find(e.u), r2 = ufset.find(e.v);
if(r1 != r2)
{
ufset.union_root(r1, r2);
ans += e.weight;
count ++;
}
}
if(count != N-1)
return -1;
return ans;
}
|
Prim算法
每一步在连接集合A和A之外的结点的所有边中,选择一条轻量级边加入到A中。使用最小堆数据结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
struct EdgeNode // 用于Prim算法的图
{
int v;
int weight;
EdgeNode(int n, int w):v(n), weight(w){}
bool operator > (const EdgeNode& e1) const
{
return weight > e1.weight;
}
};
int Prim(int N, vector<vector<int>>& connections)
{
vector<vector<EdgeNode>> graph(N, vector<EdgeNode>());
for(vector<int> e: connections)
{
graph[e[0] - 1].push_back(EdgeNode(e[1] - 1, e[2]));
graph[e[1] - 1].push_back(EdgeNode(e[0] - 1, e[2]));
}
vector<bool> used(N, false);
priority_queue<EdgeNode,vector<EdgeNode>, greater<EdgeNode>> min_heap;
int p = 0;
int count = 1;
int ans = 0;
do
{
used[p] = true;
for(EdgeNode neighbor: graph[p])
{
if(used[neighbor.v] == false)
{
min_heap.push(neighbor);
}
}
while(!min_heap.empty() && count < N)
{
EdgeNode e = min_heap.top();
min_heap.pop();
if(!used[e.v])
{
ans += e.weight;
used[e.v] = true;
p = e.v;
count ++;
break;
}
}
}while(count < N);
if(count < N)
return -1;
return ans;
}
|
单源最短路径
Bellman-Ford算法
数据结构 P379
允许输入图中包含负权重的边
时间复杂度:$O(n^2)$
Dijkstra算法
- 假设输入图的所有边权重为非负值
- 时间复杂度:$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
vector<vector<GraphNode>> graph(n, vector<GraphNode>());
for(vector<int>& edge: edges)
{
graph[edge[0]].push_back(GraphNode(edge[1], edge[2]));
graph[edge[1]].push_back(GraphNode(edge[0], edge[2]));
}
vector<int> dist(n, INF);
dist[0] = 0;
for(GraphNode neighbor: graph[0])
{
dist[neighbor.v] = neighbor.weight;
}
vector<bool> used(n, false);
used[0] = true;
int count = 1;
while(count < n)
{
int p = findMin(dist, used);
used[p] = true;
count ++;
for(int i = 1; i < n; i++)
{
if(!used[i])
{
int w = getWeight(graph, i, p);
if(w != -1)
{
dist[i] = min(dist[i], dist[p] + w);
}
}
}
}
|
所有结点间的最短路径
Floyd算法
数据结构P381









