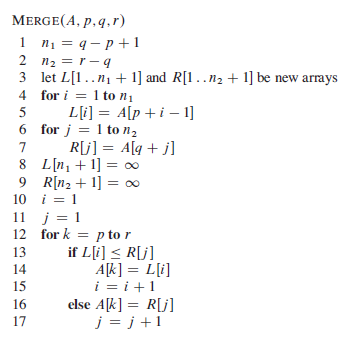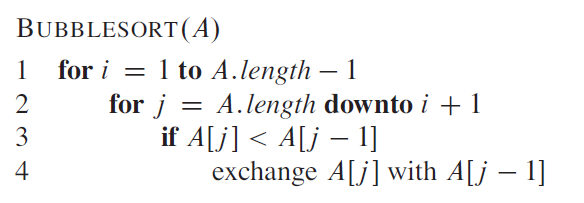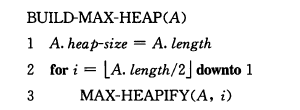与我常在

未经审视的人生不值一过

0%

【算法复习】排序和顺序统计量

发表于 更新于 分类于 阅读次数： 评论数：
本文字数： 5.9k 阅读时长 ≈ 5 分钟

排序

排序算法总结

小结

  • 任何比较排序在最坏情况下都要经过$\Omega(nlgn)$次比较，因此归并排序和堆排序都是渐近最优的

插入排序

  • 把第j个数作为key插入到A[1…j-1]的有序数列中：从后向前查找，将大于key的数向后移

插入排序

  • 时间开销：$\Theta(n^2)$
  • 空间开销：原址的（仅有常数个元素 需要在排序过程中存储在数组之外）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void InsertionSort(vector<int> &a)
{
    for(int i = 1; i < a.size(); i++)
    {
        int key = a[i];
        int j = i - 1;
        while(j >= 0 && a[j] > key)
        {
            a[j + 1] = a[j];
            j--;
        }
        a[j + 1] = key;
    }
}

合并排序

  • 思想

    • 分解（Divide）：将n个元素分成各含n/2个元素的子序列；
    • 解决（Conquer）：用合并排序法对两个子序列递归地排序；
    • 合并（Combine）：合并两个已排序的子序列以得到排序结果。

  • 辅助过程MERGE：（合并两个子数组A[p…q], A[q+1…r]）

    • 把两个子数组复制到两个新的数组L和R，合并两数组

合并排序1

  • 递归过程：MERGE-SORT

    合并排序2

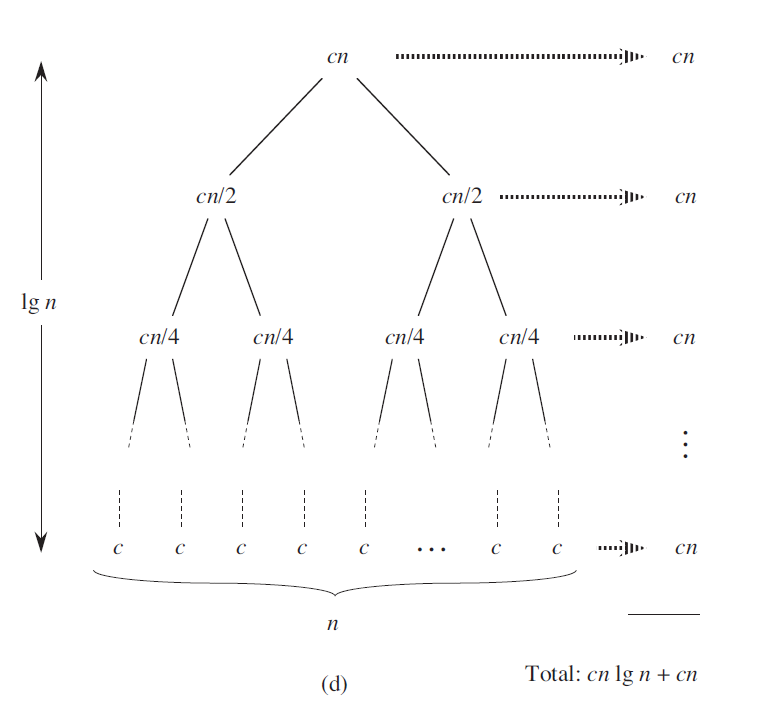
  • 递归式分析代价：

    • 递归树

      合并排序3

  • 时间开销：$\Theta(nlgn)$

  • 空间开销：非原址

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void Merge(vector<int> &a, int left, int mid, int right)
{
    int n1 = mid - left + 1, n2 = right - mid;
    vector<int> L(n1), R(n2);
    for (int i = 0; i < n1; i++)
        L[i] = a[left + i];
    for (int i = 0; i < n2; i++)
        R[i] = a[mid + 1 + i];
    int i = 0, j = 0;
    for (int k = left; k <= right; k++)
    {
        if (i < n1 && j < n2)
        {
            if (L[i] <= R[j])
                a[k] = L[i++];
            else
                a[k] = R[j++];
        }
        else if (i == n1)
            a[k] = R[j++];
        else
            a[k] = L[i++];
    }

}
void MergeSort(vector<int> &a, int left, int right)
{
    if (left < right)
    {
        int mid = (left + right) / 2;
        MergeSort(a, left, mid);
        MergeSort(a, mid+1, right);
        Merge(a, left, mid, right);
    }
}

冒泡排序

  • 思想：反复交换相邻的未按次序排序的元素

    冒泡排序1

  • 时间开销：$\Theta(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BubbleSort(vector<int> &a)
{
    for(int i = 0; i < a.size() - 1; i++)   // 已到位数字数目
    {
        for(int j = 0; j < a.size() - i - 1; j++)   //遍历剩余的相邻项
        {
            if(a[j] > a[j + 1])
            {
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

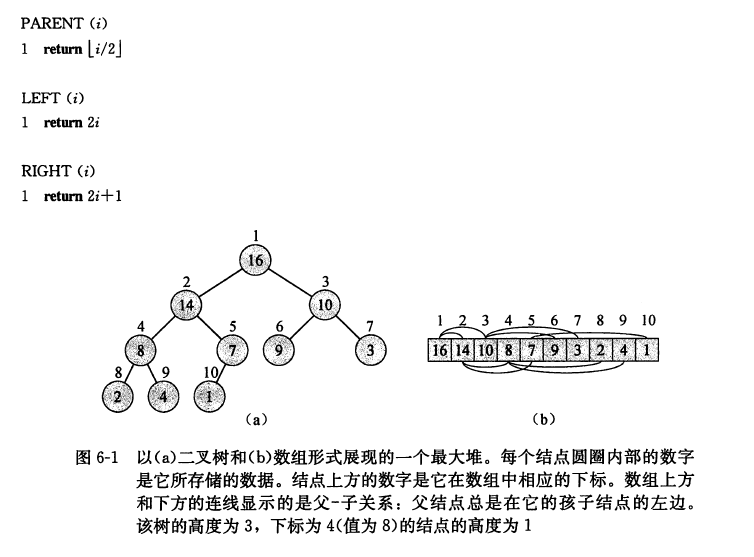
堆排序

堆

一个近似的完全二叉树，除了最底层外，该树是完全充满的。

  • $A.length$：数组长度
  • $A.heap-size$：当前有效元素个数
  • 根节点：$A[1]$
  • 给定一个节点下标$i$，计算父节点、左孩子、右孩子的下标：

堆1

堆的性质：

  • 最大堆性质：除了根节点以外所有节点$i$满足：$A[PARENT(i)]\geq A[i]$
  • 最小堆性质：除了根节点以外所有节点$i$满足：$A[PARENT(i)]\leq A[i]$
  • 树的高度：一个包含$n$个元素的堆的高度为$\Theta(lgn)$

维护堆的性质

  • 输入：堆$A$，节点$i$，假设此时以左右子节点为根的子树都已是最大堆
  • 输出：当节点$i$违背最大堆性质（值小于其子节点时），让其值在最大堆中逐级下降，从而使得以$i$为根节点的子树重新遵循最大堆的性质。
  • 在父节点、左孩子、右孩子中选出最大的，若最大的不是父节点，则将该子节点与父节点交换，对该子节点递归地调用函数。
  • 代价：$O(lgn)$

维护堆的性质

建堆

从最后一个非叶节点到根节点，依次调用MAX-HEAPIFY方法

建堆

  • 代价：$O(n)$

堆排序

首先调用BUILD-MAX-HEAP构造最大堆，此时最大元素在$A[1]$中，交换$A[1]$和$A[n]$，此时新的根节点可能违背了最大堆性质，调用MAX_HEAPIFY(A,1)，从而在$A[1…n-1]$上构造一个新的最大堆。以此类推，直到堆的大小降到2。

堆排序

  • 时间开销：$O(nlgn)$

  • 空间开销：原址的

最大优先队列

  • $MAXIMUM(S)$：返回$S$中最大键字的元素。（return A[1]）
    • $\Theta(1)$
  • $EXTRACT-MAX(S)$：去掉并返回S中具有最大键字的元素。
    • 交换A[1]和A[n]，调用MAX_HEAPIFY(A,1)
    • $O(lgn)$
  • $INCREASE(S,x,k)$：将元素x的关键字值增加到k（假设k不小于x节点原关键字值）
    • 将新关键字值不断与父节点进行比较，大于则交换
    • $O(lgn)$
  • $INSERT(S,x)$：把元素x插入到S中。
    • 在最后增加一个大小为$-\infin$节点，调用$INCREASE(A,A.heapsize,key)$
    • $O(lgn)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
class MaxHeap {
private:
    vector<int> heap;
    int getParent(int i)
    {
        return (i - 1) / 2;
    }
    int getLeftChild(int i)
    {
        return 2 * i + 1;
    }
    int getRightChild(int i)
    {
        return 2 * i + 2;
    }
public:
    MaxHeap(vector<int> array)
    {
        heap = array;
        buildMaxHeap();
    }
    void heapify(int i)
    {
        int left_child = getLeftChild(i), right_child = getRightChild(i);
        int max = i;
        if(left_child < heap.size() && heap[left_child] > heap[i])
            max = left_child;
        if(right_child < heap.size() && heap[right_child] > heap[max])
            max = right_child;
        if (max != i)
        {
            int tmp = heap[i];
            heap[i] = heap[max];
            heap[max] = tmp;
            heapify(max);
        }

    }
    void buildMaxHeap()
    {
        int i = getParent(heap.size()-1);//最后一个非叶节点；
        for(; i >= 0; i--)
        {
            heapify(i);
        }
    }
    int extractMax()
    {
        int max = heap[0];
        heap[0] = heap[heap.size() - 1];
        heap.pop_back();
        heapify(0);
        return max;
    }
    int getMax()
    {
        return heap[0];
    }

    void remove(int i)
    {
        heap[i] = heap[heap.size() - 1];
        heap.pop_back();
        heapify(i);
        return;
    }
    void increase(int i, int k)
    {
        heap[i] = k;
        if (i == 0)
            return;

        int parent = getParent(i);
        while(heap[parent] < heap[i])
        {
            int tmp = heap[parent];
            heap[parent] = heap[i];
            heap[i] = tmp;
            if(parent == 0)
                break;
            i = parent;
            parent = getParent(i);
        }
    }
    void insert(int k)
    {
        heap.push_back(-0xFFFFFFF);
        increase(heap.size()-1, k);
    }
    int getSize()
    {
        return heap.size();
    }
};

快速排序

PARTITION：将数组$A[p…r]$划分成两个子数组$A[p…q-1]$和$A[q+1…r]$，使得$A[p…q-1]$中每个元素都小于等于$A[q]$，$A[q]$也小于等于$A[q+1…r]$中每个元素。

快速排序

  • PARTITION过程

    • 选择$x=A[r]$作为主元
    • $A[p…i]$：小于等于主元的部分
    • $A[i+1…j-1]$：大于主元的部分
    • $A[j…r-1]$：尚未考虑的部分
    • 复杂度：$\Theta(n)$，其中$n=r-p+1$

  • 时间开销：最坏$\Theta(n^2)$，最好$O(nlgn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int Partition(vector<int> &a, int left, int right)
{
    int x = a[right];   // 主元
    int i = left - 1;       // i标记小于x、大于x的分界点（a[i]是最后一个小于主元的元素，a[i+1]是第一个大于主元的元素）
    for (int j = left; j <= right - 1; j++)     // j遍历每个除主元外的元素
    {
        if(a[j] <= x)
        {
            i ++;        
            swap(a[i], a[j]);        //将新的a[j]与第一个大于主元的元素交换
        }
    }
    swap(a[i + 1], a[right]);    // 放置主元
    return i + 1;
}

void QuickSort(vector<int> &a, int left, int right)
{
    if (left < right)
    {
        int pivot = Partition(a, left, right);
        QuickSort(a, left, pivot - 1);
        QuickSort(a, pivot + 1, right);
    }
}

计数排序

假设$n$个输入元素都是在0到$k$区间内的一个整数。对于每一个输入元素$x$，确定小于x的元素个数，利用这一信息，就可以直接把x放到它在输出数组中的位置上了。例如有17个元素小于x，则x就应该在第18个输出位置上。

  • 代价：当$k=O(n)$时，排序的运行时间为$\Theta(n)$

基数排序

从最低有效位到最高有效位进行排序。

基数排序2

  • 代价：给定$n$个$d$位数，其中每一个数位可能有$k$个可能的取值，若使用的稳定排序方法耗时$n+k$，那么它就可以在$\Theta(d(n+k))$时间内将这些数排好序。

基数排序

桶排序

假设数据服从$[0,1)$上的均匀分布

桶排序

  • 时间代价：$O(n)$

中位数和顺序统计量

同时找到最大值和最小值

最大值最小值

期望时间为线性的选择算法

一种分治算法，用到了快速排序中的RANDOMIZED-SELECT算法，但快排会递归处理划分的两边，这里只处理一边。

  • 算法返回数组$A[p…r]$中第$i$小的元素
  • 期望运行时间：$\Theta(n)$
  • 最坏运行时间：$\Theta(n^2)$

随机选择

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//LeetCode 215: 在未排序的数组中找到第 k 个最大的元素。
class Solution {
private:
    int Partition(vector<int>& a, int left, int right)
    {
        int x = a[right];
        int i = left - 1;
        for (int j = left; j <= right - 1; j++)
        {
            if (a[j] >= x)    // 注意这里改成了>=
            {
                i++;
                swap(a[i], a[j]);
            }
        }
        swap(a[i+1], a[right]);4
        return i + 1;
    }
    int Select(vector<int>& a, int left, int right, int i)
    {
        if (left == right)
            return a[left];
        int x = Partition(a, left, right);
        int k = x - left + 1;   // 当前的x是第几个数字
        if (i == k)
            return a[x];
        else if (i < k)
            return Select(a, left, x - 1, i);
        else
            return Select(a, x + 1, right, i - k);
    }
public:
    int findKthLargest(vector<int>& nums, int k)
    {
        return Select(nums, 0, nums.size()-1, k);
    }
};

最坏情况为线性的选择算法

与随机选择相比，保证对数组能做出一个较好的划分：

select