与我常在

未经审视的人生不值一过

0%

【论文笔记】DeepCover

发表于 分类于 阅读次数： 评论数：
本文字数： 4k 阅读时长 ≈ 4 分钟

原文：Testing Deep Neural Networks （TECS’19）

（与DeepConcolic作者相同）

代码地址：https://github.com/TrustAI/DeepCover

概括

受MC/DC思想启发提出4种覆盖标准，使用线性规划模型进行约束求解（借助DeepConcolic的方法），生成满足“独立影响”条件且变化较小的测试用例。

传统MC/DC覆盖

MC/DC是DO-178B Level A认证标准中规定的，欧美民用航空器强制要求遵守该标准。MC/DC覆盖测试在每个判定中的每个条件都曾独立影响判定的结果至少一次（独立影响意思是在其他条件不变的情况下，改变一个条件）。

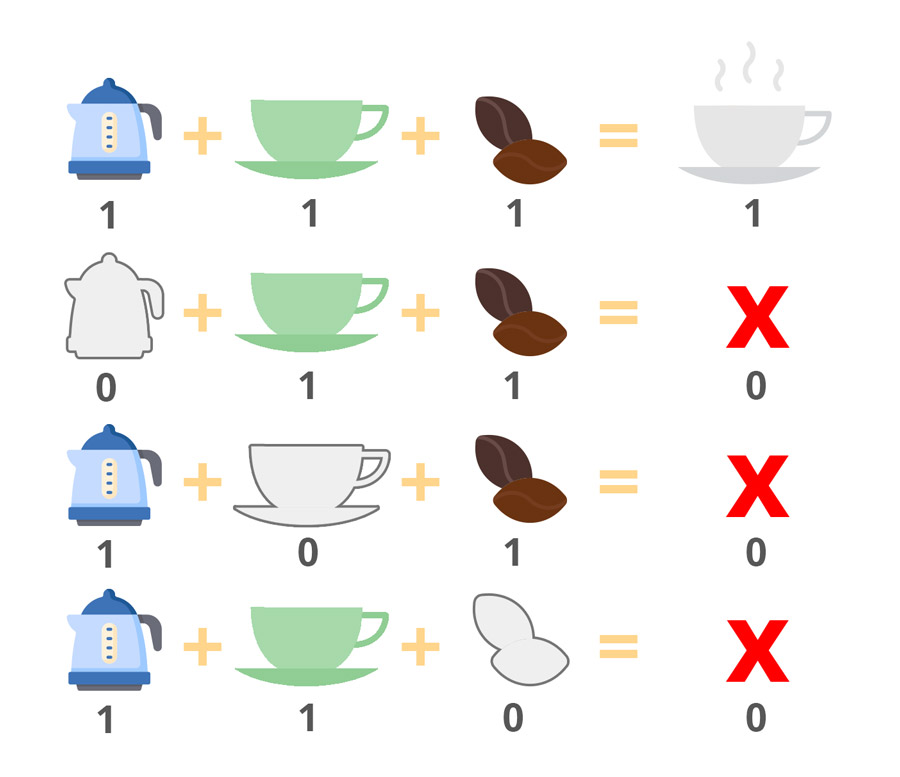
举个例子，制作咖啡需要同时满足壶、杯子和咖啡豆的条件：

1
2
3
4
5
6
if( kettle && cup && coffee ) {
  return cup_of_coffee;
}
else {
  return false;
}

三个条件的取值共有8种情况：

Fig2

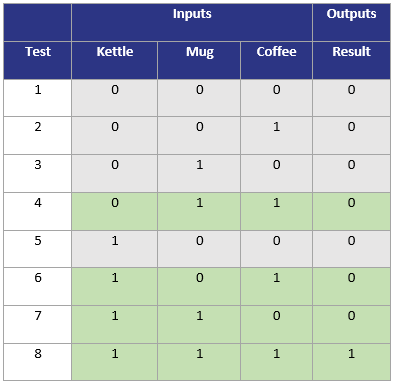
但仅4种情况（Test 4、6、7、8）就可以达到100%MC/DC覆盖率，因为：

  • Tests 4 & 8 ：Kettle可以独立影响结果
  • Tests 6 & 8 ：Mug可以独立影响结果
  • Tests 7 & 8：Coffe可以独立影响结果

Fig1

方法

DNN中的决策和条件

  • $\Psi_k$: 一个集合，其中每个元素是神经网络第$k$层节点的一个子集合，表示一个特征
    • 核心思想：不仅要测试某个特征的存在，而且要测试简单特征对更复杂特性的影响。
  • $t_k = |\Psi_k|$：特征个数
  • $\psi_{k,l} (1 \leq l \leq t_k)$：第$l$个特征
  • 每个特征代表一个决策（decision），其条件（conditions）是前一层与其相连的特征

  • 特征的使用将DNN中的基本构建单位从单个节点推广到一组节点。

  • 特征对$(\psi_{k,i},\psi_{k+1,j})$：相邻层的一对特征

  • 符号变化
    • $sc(\psi_{k,l},x_1,x_2)$：对$\psi_{k,l}$中的任意神经元 $n_{k,j}$，$sign(n_{k,j},x_1)\ne sign(n_{k,j},x_2)$
    • $nsc(\psi_{k,l},x_1,x_2)$：对$\psi_{k,l}$中的任意神经元 $n_{k,j}$，$sign(n_{k,j},x_1) = sign(n_{k,j},x_2)$
  • 值变化
    • $vc(g,\psi_{k,l},x_1,x_2)$：$g(\psi_{k,l},x_1,x_2)=true$，$g$是一个值函数

覆盖方法

  • Sign-Sign Coverage (SSC)

    • 对一个特征对$\alpha = (\psi_{k,i},\psi_{k+1,j})$，$\alpha$被两个测试用例$x_1$、$x_2$SS-覆盖，记为$SS(\alpha,x_1,x_1)$。其定义为：

      • $sc(\psi_{k,i},x_1,x_2)$ 且$nsc(P_k \backslash \psi_{k,i},x_1,x_2)$，其中$P_k$为第$k$层所有节点的集合
      • $sc(\psi_{k+1,j},x_1,x_2)$
      （即一个条件特征量$\psi_{k,i}$的符号变化独立影响下一层决策特征$\psi_{k+1,j}的$符号变化)

  • Value-Sign Coverage (VSC)

    • 对一个特征对$\alpha = (\psi_{k,i},\psi_{k+1,j})$，值函数$g$，$\alpha$被两个测试用例$x_1$、$x_2$VS-覆盖，记为$VS^g(\alpha,x_1,x_1)$。其定义为：
      • $vc(g,\psi_{k,i},x_1,x_2)$ 且$nsc(P_k ,x_1,x_2)$，其中$P_k$为第$k$层所有节点的集合
      • $sc(\psi_{k+1,j},x_1,x_2)$

  • Sign-Value Coverage (SVC)

    • 对一个特征对$\alpha = (\psi_{k,i},\psi_{k+1,j})$，值函数$g$，$\alpha$被两个测试用例$x_1$、$x_2$SV-覆盖，记为$SV^g(\alpha,x_1,x_1)$。其定义为：

      • $sc(\psi_{k,i},x_1,x_2)$ 且$nsc(P_k \backslash \psi_{k,i},x_1,x_2)$，其中$P_k$为第$k$层所有节点的集合
      • $vc(g,\psi_{k+1,j},x_1,x_2)$且$nsc(\psi_{k+1,j},x_1,x_2)$
      (捕获符号更改情况的决策特征的重大更改)

  • Value-Value Coverage (VVC)

    • 对一个特征对$\alpha = (\psi_{k,i},\psi_{k+1,j})$，值函数$g_1$、$g_2$，$\alpha$被两个测试用例$x_1$、$x_2$SV-覆盖，记为$VV^{g_1,g_2}(\alpha,x_1,x_1)$。其定义为：

      • $vc(g_1,\psi_{k,i},x_1,x_2)$ 且$nsc(P_k ,x_1,x_2)$，其中$P_k$为第$k$层所有节点的集合
      • $vc(g_2,\psi_{k+1,j},x_1,x_2)$且$nsc(\psi_{k+1,j},x_1,x_2)$
      (条件特征没有符号变化，但决策特征的值发生显著变化)

覆盖率计算

令$F= \left\{ SS,VS^{g},SV^{g},VV^{g_{1},g_{2}} \right\}$，给定DNN$N$和覆盖方法$f \in F$，测试特征对集合$O$，测试集$T$的覆盖率：

即被覆盖的测试特征对所占比例。

与现有覆盖标准的强弱关系

Fig3

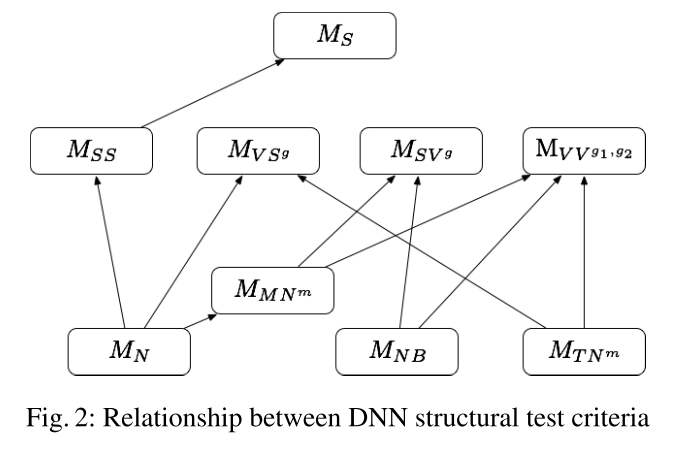
自动测试用例生成

  • 测试预言
    • $X$为一组被正确标记的测试用例，$x \in X$，若$x’$与$x$足够接近且预测标签一致，则称$x’$通过测试预言
  • 通过线性编程（LP）生成测试用例
    • 方法同DeepConcolic
  • 通过启发式搜索生成测试用例
    • 基于梯度下降搜索覆盖特定特征对的输入对

实验

数据集

  • MNIST、CIFAR-10、ImageNet

可控制参数及变量

  • LP调用时使用的约束：$\parallel x_2 - x_1 \parallel _ \infty$
  • $SV^g$中：$ g= \frac{u_{k+1},j \left[ x_{2} \right] }{u_{k+1},j \left[ x_{1} \right] } \geqslant \sigma $ ，$\sigma = 2$
  • $VV^{g_1,g_2}$中：$\sigma = 5$
  • 每个特征包含神经元个数
    • 大小用参数$w$来调节：$\psi _{k,i} \leq w \cdot s_k$

MNIST上的实验结果

  • 一个特征即一个神经元
  • 训练10个DNN（准确率>97%)

Fig4

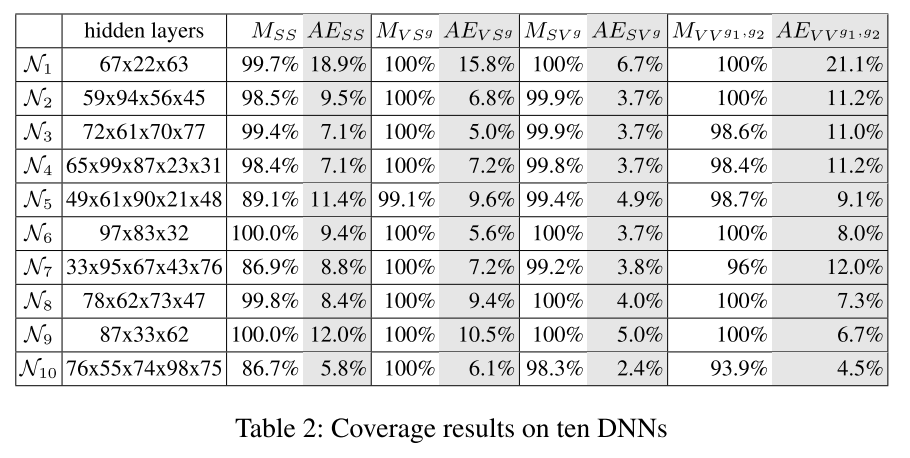
  • DNN错误查找结果：
    • 测试用例生成算法有效地实现了对所有覆盖标准的高覆盖，
    • 覆盖方法被认为是有用的，因为找出了很多对抗样本。
  • DNN安全分析：
    • 覆盖率$M_f$和对抗性实例百分比$AE_f$一起提供了评估DNN的定量统计数据。一般来说，给定一个测试集，一个具有高覆盖率水平$M_f$和低对抗百分比$AE_f$的DNN被认为是鲁棒的。
    • 下图展示了对抗样本的距离和累积对抗样本数的关系。一个更稳健的DNN将在小距离末端(接近0)有更低的形状，因为报告的敌对的例子相对于他们原始的正确输入是更远的。直觉上，这意味着需要付出更多的努力来愚弄一个稳健的DNN，使其从正确的分类变成错误的标签。

Fig5

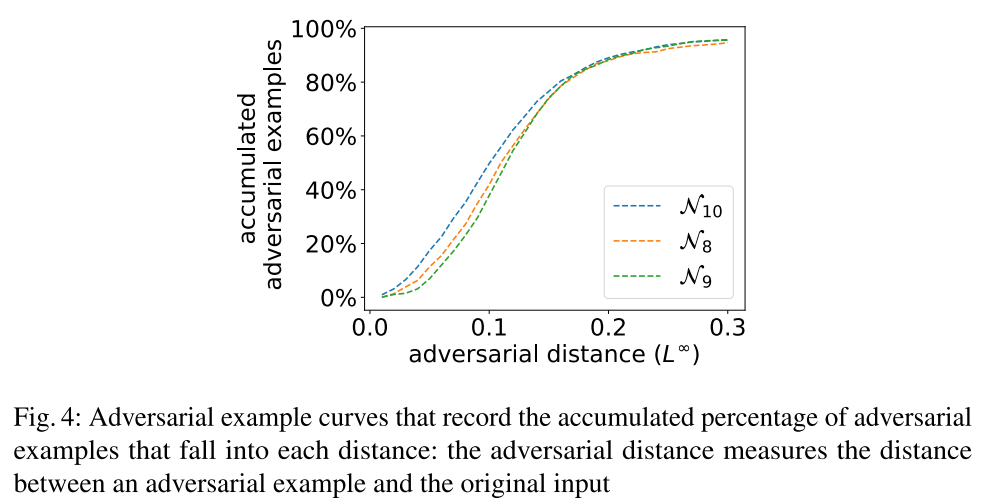
  • 逐层的行为：
    • 当深入DNN时，神经元对的覆盖会变得更加困难。在这种情况下，为了提高覆盖性能，在生成测试对时需要使用较大的数据集。图5b给出了在不同层中发现的敌对示例的百分比(在所有敌对示例中)。有趣的是，大多数对抗性的例子似乎都是在测试中间层时发现的。

Fig6

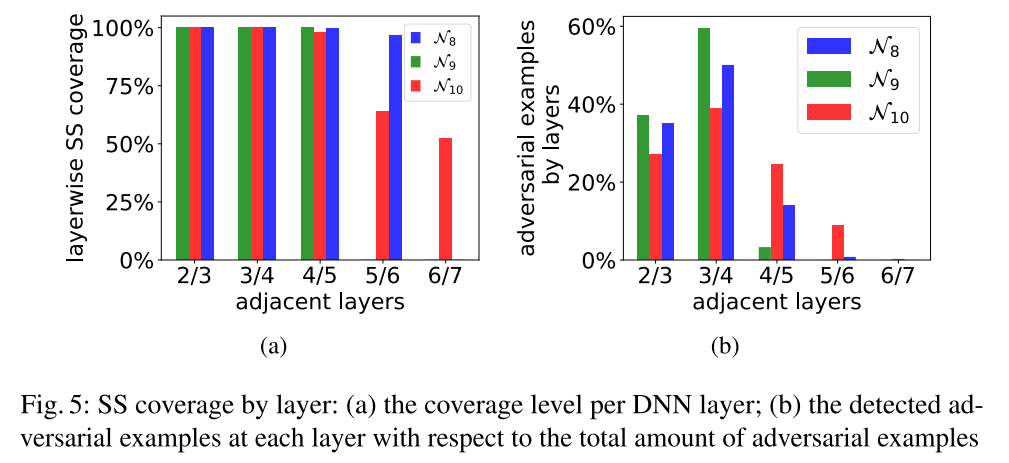
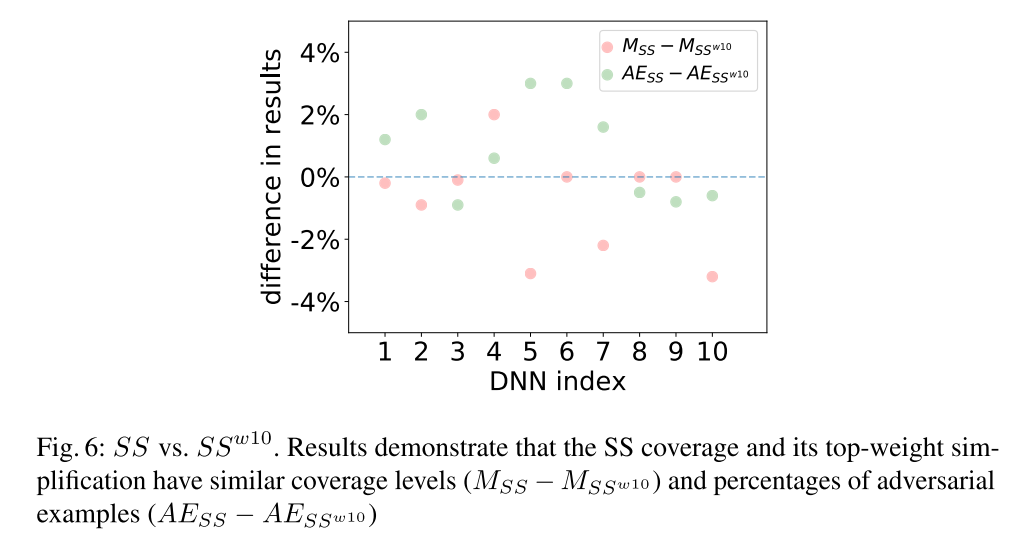
  • 高权重的SSC：

    • 为了减少测试特征对的数量，仅选择带有较高权重的一些神经元作为特征，改变前后二者的区别不大，因此实际使用时可以采用这种方式减少开销。

    Fig7

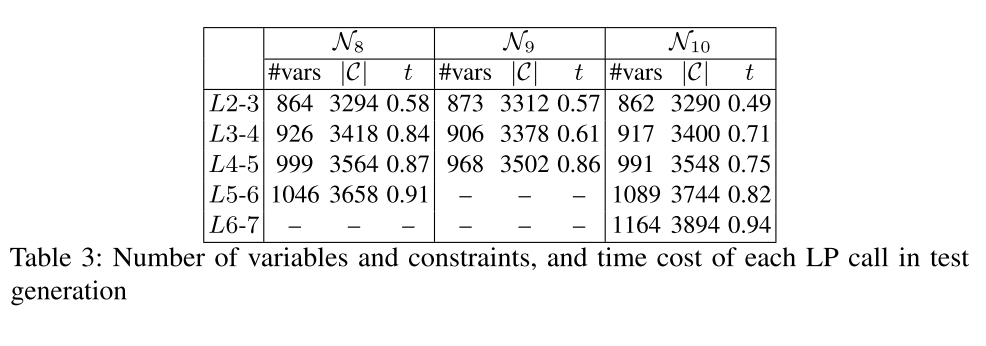
  • 调用LP的开销

    • 对于每个DNN，我们选择一组神经元对，其中每个决策神经元位于不同的层。然后，我们测量变量和约束的数量，以及在解决每个LP调用上花费的时间(以秒计算)。表3中的结果证实了部分激活模式的LP模型确实是轻量级的，并且在遍历一个DNN的更深层时，其复杂度以线性方式增加。

Fig8

CIFAR10上的实验结果

  • 在不失一般性的前提下，卷积层节点的激活是通过激活一个子集的先例节点来计算的，每个节点都属于其层中的一个feature map。我们将算法1中的启发式测试用例生成应用于SS覆盖率，并在每个不同的层分别度量决策特征的覆盖率结果。
  • 总的来说，SS覆盖率高于90%是通过相当一部分的敌对示例实现的。
  • 一个有趣的观察是,更深层的因果变化的特性能够检测小扰动的输入导致对抗的行为,而这有可能为开发人员提供有用的反馈调试或优化神经网络参数。

Fig9

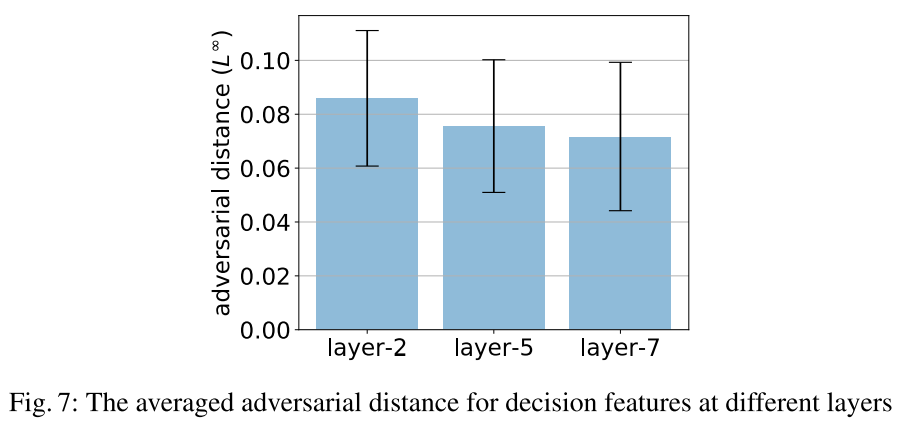
ImageNet上的实验结果

  • VGG16+启发式测试用例生成算法

  • 特征：一组神经元

    • 大小用参数$w$来调节：$\psi _{k,i} \leq w \cdot s_k$，$s_k$为该层神经元总数

  • 我们测试了2000个随机特征对的SS覆盖情况，$w \in \{0.1\%、0.5\%、1.0\%\}$。

    • 覆盖结果：10.5%，13.6%和14.6%是对抗样本。对抗样本的平均距离和标准偏差：

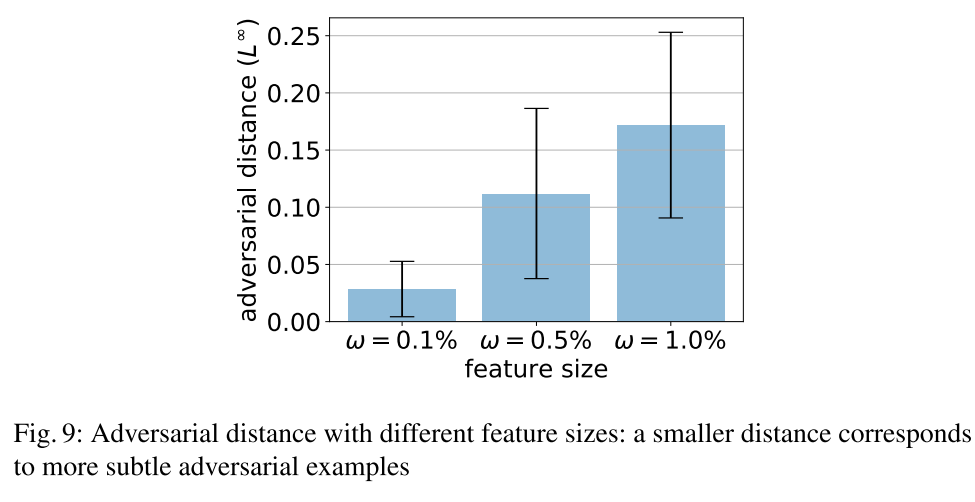
      Fig10

    • 结果表明，特征对与输入扰动之间存在一定的关系。在生成的对抗样本中，更细粒度的特征比粗糙的特征能够捕获更小的扰动。

  • 我们注意到访问边界激活值很可能要求对DNNs进行更大的更改。我们设置功能大小使用$w$= 10%,获得的测试集中有22.7%的对抗样本。然而，这些敌对的例子的距离，平均L∞-norm距离3.49，标准差3.88，远远大于SS覆盖的距离