原文:Symbolic Execution for Deep Neural Networks (ISSRE’18)
代码:没找到
概括
提出DNN上的符号执行测试方法。将DNN转换为程序(激活函数转换成if-else),利用相关性识别出重要像素。约束求解器求解激活模式相同但预测标签不同的输入(改变重要像素的值)。
动机
传统软件测试的符号执行
软件测试中的符号执行主要目标是: 在给定的探索尽可能多的、不同的程序路径(program path)。对于每一条程序路径,(1) 生成一个具体输入的集合(主要能力);(2) 检查是否存在各种错误,包括断言违规、未捕获异常、安全漏洞和内存损坏。使用符号执行分析一个程序时,该程序会使用符号值作为输入,而非一般执行程序时使用的具体值。在达到目标代码时,分析器可以得到相应的路径约束,然后通过约束求解器来得到可以触发目标代码的具体值。
在DNN上使用符号执行的挑战
- DNN没有分支
- DNN高度非线性,没有约束求解器
- 扩展性差:DNN神经元数量庞大,远远超出了当前符号推理工具的能力。
我们的方法:
- 将ReLU激活函数看作if-else语句,这样DNN就有了分支
符号执行框架
翻译DNN:
将ReLU函数转换为分支语句,则一个神经元可以看做代码段:

识别重要像素
维护一个相关性数组$coef^h_{i,j}$:$h$层第$i$个神经元与输入中第$j$个像素的相关性
初始化:若$i=j$,$coef^0_{i,j}=1$,其他为0
迭代计算coef:

最终输出单元的Coef计算结果为:
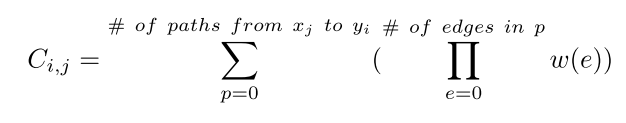
从像素$x_j$到输出$y_i$的所有路径(输出非0)上所有权重的总和(依赖于给定输入集合的具体执行)
然后我们计算每个输入变量重要分数,使用三个指标:
- $co$: 相关性分数,即$C_{i,j}$
- $coi$:相关性分数乘以对应的输入变量:$C_{i,j} \times x_j$
- $abs$:相关性分数的绝对值$|C_{i,j}|$
确定攻击像素
构造约束求解问题:改变像素的值,使得新图片与原图激活模式相同,但预测标签不同。使用约束求解器Z3求解。
激活模式相同:($H$为神经网络中所有激活函数的个数,即每个神经元激活模式都保持不变)
$ PC= \land _{h=1}^{H}(B^{h}+ \sum _{i=1}^{t}C_{i}^{h} \cdot X_{i} \gamma 0) $ , 其中$ \gamma \in \left\{ > , \leq\right\} $
预测标签不同:($l’ \neq l$)
约束:$ RA= \land _{1}^{t} lo \leqslant X_i \leqslant hi $ ($lo$和$hi$是输入值标准化后的上下界)
最终约束求解器目标:$PC \land AC \land RA$
攻击
- 1像素攻击
- 2像素攻击:对前5%的重要像素的任意两两组合进行约束求解。
实验
实验配置
- 数据集和模型
- MNIST
- 模型结构:784×10×10×10×10
- 训练集:60000张图片
- 准确率:92%
- 选择训练集里的10张图片(0-9)作为原始图片种子
实验1:重要像素识别效果
- Top 5% 和10%重要像素识别结果
- 总的来说,符号执行的使用能够识别重要的像素,这有助于解释神经网络的分类决策。

实验2:用符号执行进行1或2像素攻击的效果
- 对1像素攻击:首先穷举每个像素(共784个)来确认其是否可攻击(改变像素值后激活模式不变,但预测标签改变),10张图片的可攻击像素如下:

1-像素攻击:10个数字可攻击像素的个数和最小可攻击像素的ID(即穷举搜索需要尝试的个数)

2-像素攻击:
- 许多2像素攻击由一个可攻击1像素的像素组成。然而,一些新的攻击对不包括任何像素可攻击的像素被发现为1像素攻击。

实验3:比较识别出的重要像素和攻击使用的像素
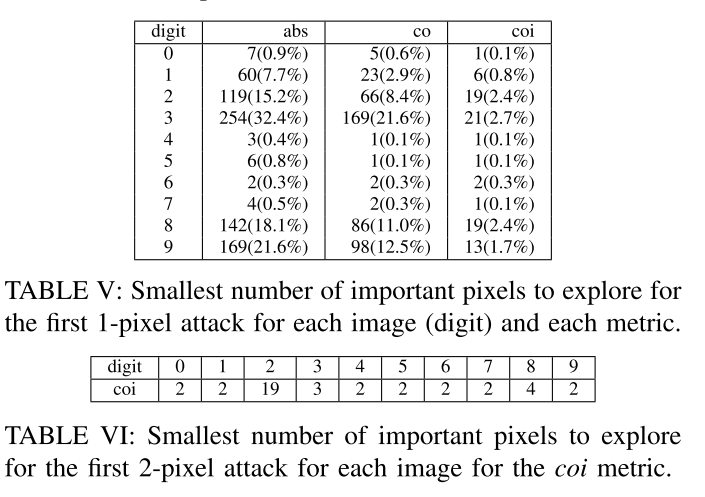
- 表V显示了对于每幅图像,在发现1像素攻击之前,三个指标中的每一个都必须探索的重要像素的最小数量。对于所有指标和所有图像,需要检查的重要像素不超过前三分之一,以找到攻击像素。
- coi识别效果最好。
- 总的来说,利用本文重要像素识别算法,对于寻找1像素和2像素攻击具有重要作用。
可控制参数及变量总结
- 重要像素百分比(如5%、10%)
- 初始种子集合:10张图片
- 重要像素判断指标:$co,coi,abs$
- 攻击像素个数
思考
本文将DNN转换成程序从而获得执行路径的方法或许值得借鉴。
但开销过大,只能在小型数据集和模型上使用。